For parents and non-professionals assisting KS4, years 10 and 11, CIE 0580 IGCSE maths, international students

What’s the problem?

As a parent, it can be difficult to know how to help your child, even if you have a talent for maths yourself. They always seem to be taught it differently from how you were taught, and you fear you might make things worse not better. With this topic, have no fear!

Those students who are falling behind at KS4 level (years 10 and 11) are in need of a change in their mindset. Their technique of studying maths is more likely the problem than their ability to grasp the concept. Instead of studying by just reading their notes and answering questions, they must engage in active learning. Success surely follows.

Active learning equates to 

1. Learning the vocabulary

2. Practicing reading out loud anything containing symbols e.g. square root

3. Memorising the list of The Square Numbers

4. Identifying all the different ways of saying the same thing 

5. Learning by heart the pairs of square numbers and their partner square root

6. Putting imagery in place  of some practical applications eg area of a square in geometry

7. Connecting this topic to other related topics and anticipating cross-topic questions.

Students will have met square numbers and square roots annually, beginning year 5 in the UK and anyone who hasn’t mastered this topic by year 10 most likely will not know the vocabulary. They confuse being familiar with the sound of the words with knowing what they mean. It makes no difference whether the student speaks English as their first or their second language. Square and square root sounds oh so familiar, like old friends, but ones they have lost touch with!

Let’s consider each point in turn. Possibly you yourself have a solid understanding of this topic and are overseeing your child's work. Here I am not teaching the topic, rather offering practical tips on how you can help your child to learn square numbers and square roots .

Learning the vocabulary.

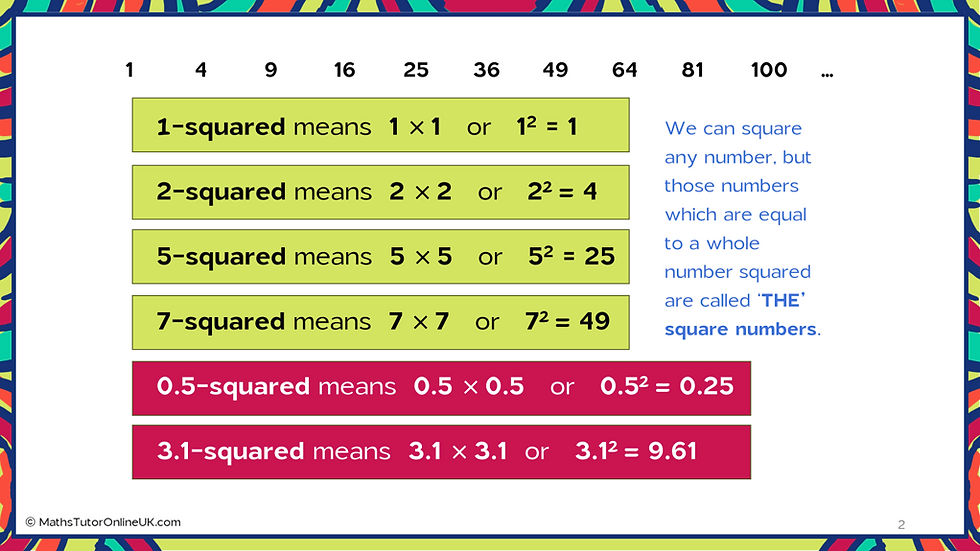
Facts they don't always appreciate.

• ‘A square number is a number that is equal to a whole number multiplied by itself.

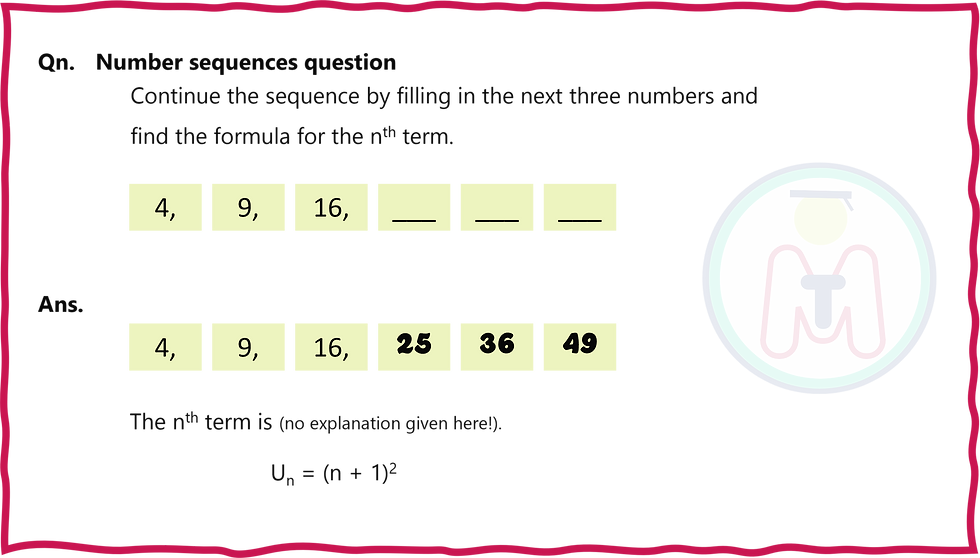
• ‘The Square Numbers’ is the list “1, 4, 9, 16, 25,...”  It is infinite (i.e. one that goes on forever and never ends) and the numbers are listed from smallest to largest, To speak about only one number on the list we would say for example that ‘9 is a square number’, with emphasis on 'a'.

• Notice, we can take any number and square it. However, the result will not be a whole number and so the result cannot be called a Square number. 

• Square roots are the partners of squares. It means if we find that 5 squared equals 25 , then the partner statement is 'the square root of 25 is 5' - automatically..

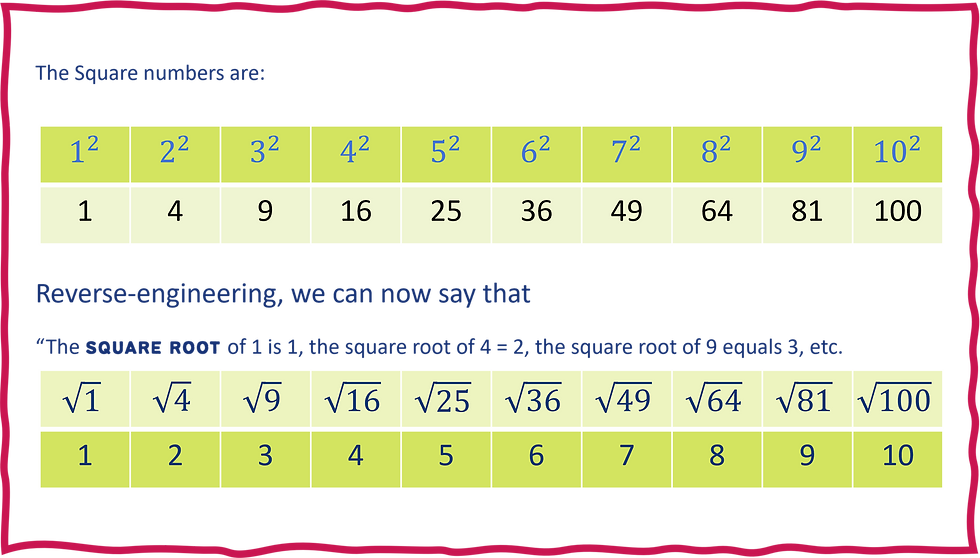
Reading maths that contains symbols

Reinforce the idea that writing in maths is literally shorthand for what we say in words. Students sometimes shy away from reading equations, especially those containing square root symbols and powers or indices. They quietly ignore any request to explain the middle steps, only supplying the final answer. If they get it right anyway, what is the problem? Often it signals a hazy grasp of the connecting concepts and i

results in only limited ability to answer harder questions, especially wordy ones.

Don’t underestimate the importance of speech in maths. After all, it is a language. I remember having a lightbulb moment when I was learning to read. After a few days of stumbling over a few similar words, the penny suddenly dropped. They were actually ones that was already using in conversation. Making the connection was awesome. A similar disconnect exists between reading and speaking maths. Expect lightbulb moments!

It helps if you write alongside anything containing symbols. You should state ‘in maths we write, and in english we say: … ‘

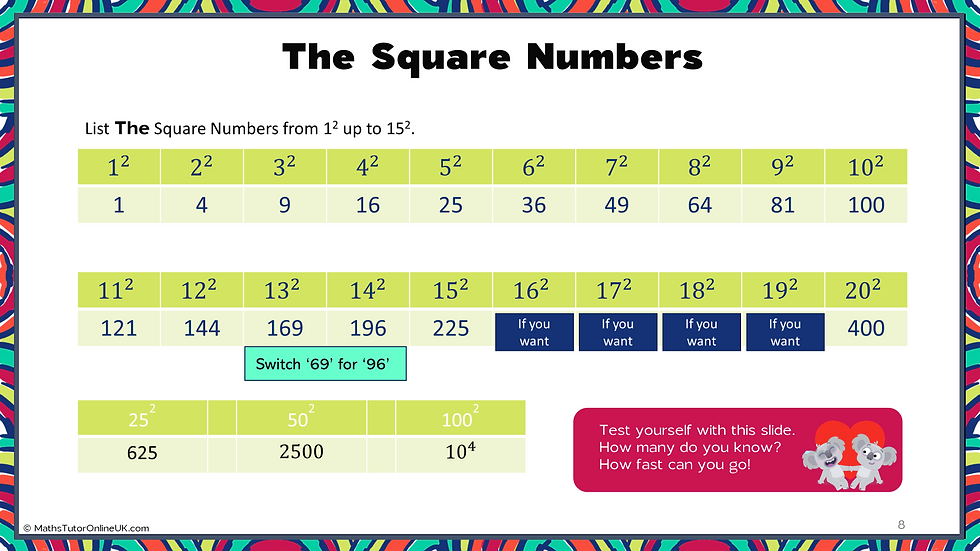
Learn the list of THE square numbers

Hot tip: memorise the first 15 numbers on the list just as you do the times tables. They are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225.  They will benefit from also knowing that 202 = 400 and 252 = 625.

Practice different ways of saying the same thing

In an English language lesson an example of this would be that ‘if Anna is the mother of Paul’ then, automatically, we can also say that ‘Paul is the son of Anna’. ‘Automatically’ being the operative word. In a maths class we could offer this as an example:  Since ‘4-squared equals 16’, we can automatically also say that the square root of 16 equals 4. 

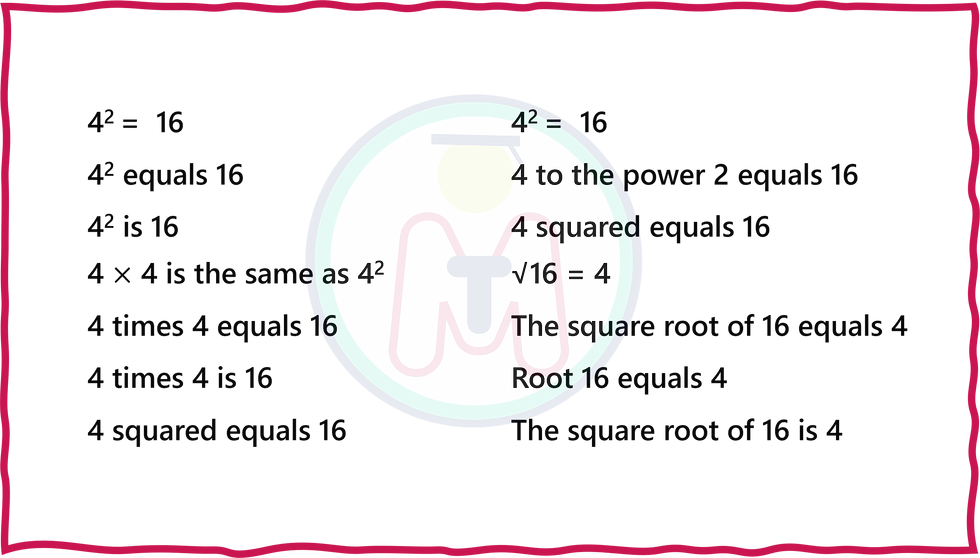
Without any further work, it could also be said that

4 times 4 equals 16, 4 times 4 is 16, 4 to the power 2 equals 16, the square root of 16 is 4, root 16 equals 4 etc. 

Learn by heart the pairs of squares and square roots

Ideally, if you say 5 squared equals 25 the student can respond that the square root of 25 is 5. Once they have that pattern you can ask them about one they have never met before. For example, the square root of 676 equals 26, according to the calculator. The partner statement would be that 26-squared equals 676.

Students are expected to remember the ones at the beginning of the list of square numbers. It almost goes without saying that students who do not memorise them will not know the pairings. They will be left wondering how they were supposed to know that!

Imagery of some practical applications

In geometry, the area of a square is calculated by multiplying the length of a side by itself.  Though they know and use this result unaided, it turns out they don't really get what area is in practical terms. You can clarify this by using squared paper if necessary. It is important they can work backwards too. That is, find the length of the side of a square when given the area. The imagery of squares also brings clarity to the concept of approximate values of square roots.

Connecting this topic to others

1. The square numbers often feature in the topics of number patterns and in questions on indices. (Indices is the plural of index and other words for index are power and exponent.) We can expect students to recognise the pattern of the square numbers but would rarely expect them to recognise random decimal numbers squared such as 3.142-squared say!

1. Many square roots are irrational numbers. Irrational numbers are numbers that cannot be written as a fraction. We recognise them as decimals that go on forever without recurring. The square root of any prime number is automatically an irrational number.  e.g. 5  and  11 We just have to learn the list of prime numbers so that we can suggest examples to give.

2. Watch out though!  Since 3 squared equals 9 we can check that 0.3 squared  = 0.09 and so The square root of 0.09 = 0.3. Since 0.3 can be written as a fraction 0.09 it is not an irrational number. 

3. Another way of writing root 5 is 5 to the power of a ½ 

General tips for improvement in maths in years 10 & 11

Students at this level are expected to appreciate how each topic integrates with other topics. Imagine teaching someone how to utilise material that they don’t have any memory of. Your journey together will resemble a slow-motion train crash. 

1. Make a special effort to have them interact with you verbally. They often don’t appreciate the difference between simply recognising words and understanding their meaning. I can relate. When I was at school (a while back now!) I knew that ‘fille’ and ‘garcon’ were the french words for boy and girl. Hard as I tried, I couldn’t always remember which was which! It was very frustrating to know so many words and still not understand anything much.

2. Spend time building up speed and accuracy and explain the reasoning behind it. If a student is not motivated to practice because they understand the material, they often can’t retain it for very long. They don’t know this. Use rapid fire questions about only the material they need to memorise such as pairs of roots and squares to go against the clock! Keep it light-hearted game and have a laugh together.   It is also a way of assessing anyone you feel awkward about asking basic questions. 

3. Encourage them to use this form of exercise with their classmates when appropriate. too slow and they switch off.! Anyone who has learnt how to ride a  bicycle will identify with this - sometimes going too slowly can cause you to fall off! 

What next

You might like to take this quiz on square numbers and square roots to find out how much of an expert you are already. If you get top marks you don’t need my help!

Alternatively, if you are interested in teaching this material I have created a PowerPoint and worksheets that complement each other. They are available as a single product via my store Digital Maths Tutor Online hosted by Teachers Pay Teachers.