Crack the Code: Mathematical Problems & Order of Operations
Updated: Jun 29

IGCSE Students can tell you that BODMAS/PEMDAS rules relate to the mathematical Order of Operations. But do they know how to properly apply the rules? Some do!
Teaching it
Order of mathematical operations is a fundamental skill for transitioning from basic elementary mathematics to any higher level. The method I use to teach it works perfectly for tutors and students who connect online, usually 1:1 and occasionally in small groups. Parents may be interested too.
These students are following the Cambridge IGCSE 0580 or (US) 0444 mathematics syllabus (age 14 to 16), although the whole process is readily adaptable to traditional classroom settings. Either way, prepare to celebrate success!
Setup for online tuition
I use a Samsung Galaxy Tab S7 tablet (previously I had a Galaxy Tab A (2019) with stylus) connected to my laptop via the APowerMirror app. It means I can create handwritten notes in a OneNote or Samsung Notes app during the lesson. Both Skype and Zoom allow the tablet to overlay the desktop during screen sharing. In that way students see the presentation material and the note-taking app together. Whenever I ask them to help solve something they tell me what to write and I do the writing. By the end of the lesson we have generated a tailor-made set of notes which they have access to 24/7.
It works brilliantly as they get to practice ‘speaking maths' while I set about identifying their weak spots and providing supplementary information. It is a win-win situation. Google Classroom is an ideal place to store all of the links and you don't need to be part of an organization to use it.
Bringing BODMAS Centre Stage
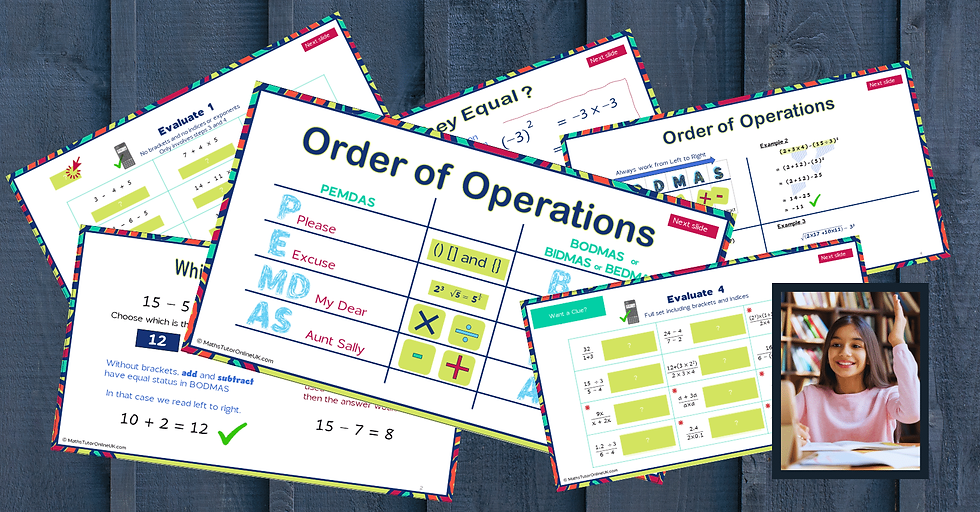
Most IGCSE students already know the mnemonics of BODMAS and PEMDAS for the rules of order of operations. Their problem is in applying them. A digital presentation has the advantage that it can include moving parts and is more visually stimulating. With a digital presentation, you can store the visuals, common misconceptions and exercises, all together in one place.
I begin with a simple question and a choice of two possible answers. e.g. ‘Calculate 5 + 8 x 2.” Is the answer 26 or 21? Whichever they give, we will talk about how and why someone else might have chosen other one.
The more ‘obvious’ answer is obtained by reading from left to right and calculating step by step. i.e. 5 + 8 = 13, then 13 x 2 = 26. Working online, it’s easy to show them that Google gives 21 as the answer! How so? Why not 26? If your students are seeing this for the first time you can have so much fun with this. Might Google be wrong?
Older students are less impressed! They already know there is a catch. They may not realise that algebra is the root cause of this problem. We know that when substituting a value in place of x that 4 + 2x gives the same result as 2x + 4 and that 2x always means 2 times x. Try it with x = 3. Now the penny drops.
Multiplying before adding ensures 2x is accurately processed. We cannot have a different set of rules depending on whether our calculation involves algebra or not, so everyone agrees ‘by convention’ to use the same. Whether we call it BODMAS or PEMDAS or BIDMAS, BEDMAS or even GEMS is unimportant.
Common stumbling blocks
In IGCSE tutoring sessions the aim is to dismantle wrong thinking and effect a reset. Generally, more competent students will not have difficulties with this topic. However, it is important that all of them undergo a check-up at this stage, and this is as easy as trying the question sets in the presentation.
Students who consistently come up with the wrong answer will comment
“I don’t get orders ( or exponents in the US) and why isn’t there a rule for roots?” They confuse the meaning of order and interpret it literally instead of as an alternative word for power or index or exponent. Anyone not familiar with the fact that roots can be rewritten as fractional indices will also falter here.
“How can you simplify brackets first when there is addition and multiplication inside the bracket itself?” This can be fixed by practicing questions that don’t contain brackets before moving on to ones that do.
“Reading from left to right in some situations seems meaningless as that is what we are doing anyway.” These students don’t fully appreciate that every new line of workings needs to be reassessed beginning with B again then O then D etc. This type of confusion occurs as a result of them not writing all the details at each and every step. Shortcuts lead to arithmetical errors.
These are helpful pointers to the type of wrong thinking responsible for the difficulties. Students who have weak basic numeracy skills often have limited mathematical vocabulary. It is super important to repair this and well worth the effort.
During the lesson
An anchor chart or similar visual will make it easier for them to follow along. Online or digital tools can have moving parts, allowing students to better appreciate the message.
To avoid confusion, stick with one mnemonic. I use BODMAS. B = brackets (equal to P of PEMDAS where P = parentheses) O = order (equal ‘power’ or ‘root’) In the other mnemonics it would be that O is equivalent to I = index and E = exponent in BIDMAS and BEDMAS).
In a one-to-one setting, you can ask what they remember and build on that. Use a few examples as something to point at. It is important you show at least one sufficiently complicated question. Otherwise, they won’t see the benefit of knowing the rules. It will be too trivial.
Guided practice working online one-to-one
This will likely turn out to be ‘working together’ on further problems. Begin with questions that contain neither brackets nor powers and work in stages. Move on to those with brackets, but not indices and finally, introduce powers and roots. Mostly students are taught BODMAS applied only to integers. Check your syllabus, because in the US for example IGCSE 0444 students also need to apply it to fractions and decimals.
If you are working online and your student(s) cannot focus, have them copy whatever you're writing on your tablet into a dedicated tuition notebook or file. It helps. Be sure to tell them to copy exactly what you write and add in their notes afterwards if they want to. Just for this exercise have them write more not less. By writing more lines of work there are fewer changes to keep track of on each line for future reference.
Of note
It is worthwhile to explain why division and multiplication have equal status. Both are two sides of the same coin in truth. Do they know that “divide by 2” is the same as “multiply by a half”? If your students have a hard time grasping this, give them some examples that only contain multiplication and division and have them randomly place brackets and recalculate. They will notice the answer is always the same.
Addition and subtraction follow similar logic. Subtracting adding the negative counterpart. e.g. “5 - 3” is the same as “5 + (- 3)”.
Parentheses Brackets and Braces
Some mathematical education websites try to distinguish between these three, claiming there is an order in which they should be addressed. This is not true. The only rule it makes sense to follow is
regardless of where you put parentheses ( ), brackets [ ] or braces { } you can't do anything else but simplify the innermost first.
I have been teaching maths at many levels for more than 30 years and have only come across this distinction in 2024! As a matter of interest, I am from the UK and have grown up calling parentheses brackets. They are all brackets to me, normal, square and curly. :) If you are a coder there could well be a precedence but we need not complicate our lives in middle and high school math (or secondary level maths in UK-based systems).
This has become quite topical recently as many parents and teaching assistants are looking for clarification. If you have anything to contribute please do comment. When we share knowledge everyone benefits.
Practice and Perfect Order of Mathematical Operations

Now the students have a good understanding of the rules and are clear about how and when to apply them we move on to practice and perfect their craft. Working online you could incorporate the graded exercises within the presentation for simplicity. I do.
I have some full slides that contain questions with answers hidden beneath a mask. When I click on the mask the full solution lies underneath. It is a time-consuming process, but once complete the students can use it again and again and it offers immediate feedback.
So often a new student will tell me they have to prepare for a test and need to revise 8 or 9 topics in the space of 40 minutes! Only when we start that process do they realise they barely remember any of the material. They are shocked because they don’t realise how easy it is to lose knowledge, and how fast it can happen. Test-prep becomes re-learning rather than consolidation. For this reason, I make sure I advise them of this phenomenon.
Whatever you provide them with up to this point is good for test-prep and revision purposes too. It will save you the time of looking for yet more questions and making an answer sheet to go with it. They will have everything they need in one place too.
If you prefer they practice away from electronic devices worksheets and task cards are ideal alternatives. If you are not familiar with task cards read on.
Thoughts and Questions

During any process of creation inevitably questions pop up. You might be interested in these.
Differentiation
If you don’t know, differentiation refers to making sure you engage all students fully, regardless of their ability. That way more able students are not left twiddling their thumbs during the last part of each lesson. If you are using task cards or worksheets this is easily achieved.
Tip: Often people print task cards on different coloured paper/card depending on difficulty level as it helps with sorting.
Find your level
Know your syllabus. The CIE 0580 IGCSE maths syllabus can be found here, the CIE (US) 0444 IGCSE math syllabus is found here and the National Curriculum for children of all ages in the UK is found here.
I give students a copy of the presentation I made for our online lesson and which contains many graded questions. The questions are marked as to which level they apply. It will either be Core or Extended. Sometimes the UK-based and US-based IGCSE versions have different specifications. This topic is one place they differ.
Printables
Even while working online, printable worksheets have value. PDF files can be displayed online and used for teaching or homework. They can also be printed by students and used away from electronic devices. Afterwards they can be stored for revision and test-prep. If you buy printables check whether your purchase includes the popular ink-saving black and white versions.
Have you noticed, the older the student, the harder it is to find exercises that match exactly what you have been working on with them during tuition? Chances are, basic numeracy skill practice will not be appropriate for IGCSE students. It will either be too simple, or too complicated and likely include other topics they are rusty on. It can leave them feeling they have not learnt anything after all. Better to write your own.
Anchor charts are a great way of assisting your student to retain knowledge in the long-term. Sometimes you find them for sale separately, and other times as part of a package or bundle. Essentially they are visual summaries of a topic, a little like a mind map. Teachers sometimes plan them and complete them as they progress in a lesson. Other times they give the student a blank copy containing the bare outline and the student completes it however they see fit. They can even be fixed to the wall in class.
Gamify
Anything you can do to lift the spirits of the student without them losing focus is a plus. The questions contained in my presentation can be revisited and points awarded for correct answers, with extra points for harder questions. You could alternatively put a time limit on answering. If you have a larger group, you could split them into teams for this.
Anyone wanting to stay away from their laptop could use task cards instead. It could even work with the family at home. Parents versus children maybe!
Need help?
If you are short of either time or energy or both and would like to own the same materials that I use, follow this link by clicking on the image.
This site may contain links to affiliate websites and we receive an affiliate commission for any purchases made by you on the affiliate website using such links.
We are a participant in the Amazon Services LLC Associates Program, an affiliate advertising program designed to provide a means for us to earn advertising fees by linking to Amazon.com and affiliated websites.


Comments