Metacognition and self-regulation in learning maths

Parents, are you concerned about how maths is taught in school? In the best places metacognition skills are actively  taught  in tandem with the math content.

Metacognition and self-regulation

Metacognition is typically understood as the process of ‘learning how to learn’. Ironically, metacognition is not easy to teach! It is highly intuitive and nuanced. Students improve in this area by setting goals, self-monitoring and by working strategically. 

Self-regulation is the ability of an individual to understand and manage their behaviour and their reactions to feelings and things happening around them. Students who have mastered self-regulation are aware of their strengths and weaknesses and the strategies they use to learn.

Improving metacognition and self-regulation are both considered high impact, low cost strategies. Economic winners! It turns out that students from disadvantaged backgrounds benefit significantly more from being taught these skills.

All students who master them are better at self-evaluating the effectiveness of their learning and experience  accelerated growth. As students become more tuned in to what they do and don’t know their resilience improves, energising them to learn more. This fosters a growth mindset and improves motivation.

Metacognition in Maths

The focus here is on middle- and high-school level students - essentially teenagers. Math(s) is one of the hardest subjects for students to handle when they don’t understand the material. They need to learn what to do when they don‘t know what to do. But how do you improve metacognition in maths?

Broadly speaking, educators are primed to promote discussion during classes and to follow-up by having students reflect on their learning afterwards. Students ought to be advised in advance of new topics and given a chance to do some preliminary work, before being taught in class.

Ideally educators will model different strategies, explaining their thinking as they go, similar to a TV producer whispering in the ear of a presenter during a transmission. They will pepper their presentations with questions on basic fact recall, what to do next, and why some things would not work. 

Open-ended questions are best, and you should not imply there is only one way to do anything. You don’t want to keep asking ‘Are you sure?’ either. Keep it light and give students plenty of time to think and consider what might be a good response.

Roles can be reversed so the student has a chance to share their thoughts. Describing what they have learnt brings them clarity and simultaneously provides an opportunity for the educator to correct misconceptions. 

Elements of the Ideal Lesson

Pack Metacognition strategies into your maths lesson

Do it like this!

1. Activate prior knowledge

Construct a framework from which to hang the new material. It need not be anything heavy. A short quiz would suffice. Don’t make the questions too difficult because we also want to build up their confidence and make them optimistic about being able to master the new material. 

2. Explicit strategy instruction

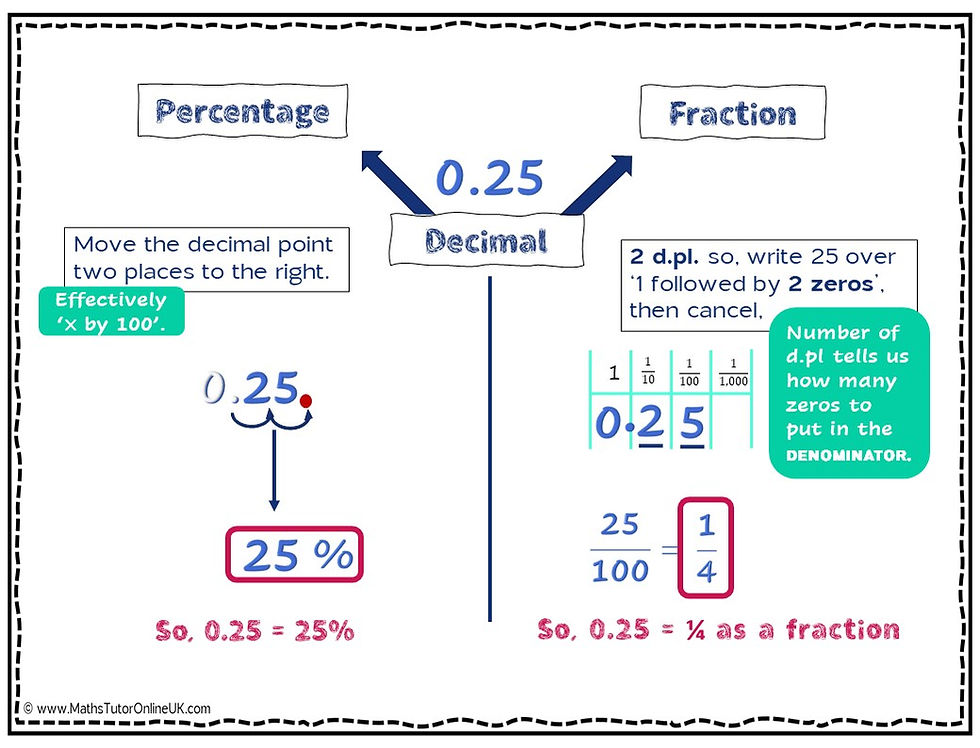
This will be teacher led and consist of clear worked examples with notes that detail every step. During this phase, you can ask metacognitive questions such as ‘ How else could we represent ….?’ and ‘How can you check your answer?’ or ‘What might some students get wrong at this stage?’

If you have a chance to tailor the presentation closely to the ability of the student, do it. For example, working one-to-one, you might provide some worked examples with only partial information and ask them to fill in the gaps.

Failure to challenge will result in a loss of focus and deterioration in performance over time. They become underwhelmed and bored. 

E.g. Someone who has covered fraction addition many times and still has no concept of equivalent fractions would be taught procedurally, as if following a recipe. On the other hand, a mathematically fluent student, should be encouraged to look out for opportunities to use shortcuts and strategies from mental maths.  If you teach the fluent student step by step instructions you lose the opportunity to interest them in free-thinking and problem-solving

3. Modelling of learned strategy. 

One of the most effective strategies for teaching maths has been in the presentation and discussion of worked examples. Even students who find math(s) particularly difficult will benefit from this.

Again this is teacher led. Explain your thinking out loud to the students and ask them their opinions. 

4. Example - problem pairs 

These example-problem pairs are a tool to highlight different cases. On one side of the whiteboard the teacher writes the worked example and on the other they write a similar question for the student to practice alone. 

The teacher talks the students through the example - “The first thing I would try is …” “Then I would check …” “Then I would     to see if my answer makes sense.” It is important the student appreciates the value of checking that their answer is a credible one and that their thinking is joined up.

5. Memorisation of learnt strategy

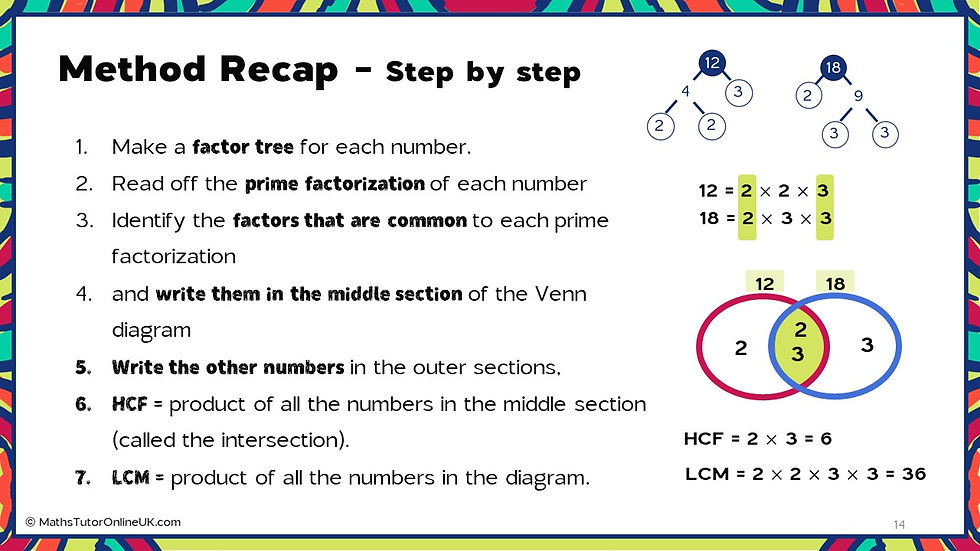
In the beginning, let students refer to their notes because they will not have had a chance to memorise anything yet. Using notes reduces cognitive load by shifting their thinking to applying the strategy rather than remembering it.

They must not skip memorising though. Success at this stage   signals they have assumed a higher level of personal responsibility for their learning. 

Homework can provide a great opportunity for students to memorise. I often have students try to memorise in class. Read their notes and then close their book and tryto write down as much as they can remember. The few minutes it takes from the lesson is well worth it. Sending them home and telling them to memorise it is often quite hopeless.

Questions you should ask here are ‘How do you know which strategy to use?’ and ‘What is the first thing you could do just to get started?’

6. Guided Practice 

Here the student does the work and the teacher can either provide simple verification feedback. i,e. Only tells the student the actual number or word that is the answer, not the explanation. Or full solutions. The full solutions are better in a way as they can be used as a learning tool that helps the student reflect on their current level of knowledge. They also serve as practice material for revision and test prep and supports them in independent learning.

7. Independent Practice 

This is student-led and students aren’t asking the teacher for constant reassurance. It is a crucial element of the learning process for any students wishing to become self-regulated. Here, they get to choose, manage, deploy, monitor and evaluate metacognitive skills all by themselves.

Always include an enrichment question. e.g. ‘How many ways can you find of doing …..?’ or ‘Next lesson we will be learning …. How might we go about that?’ Enrichment questions put the student in the teacher’s shoes in the sense they need to satisfy themselves they are making the right decisions.

At the end of the lesson dedicate a few minutes to reflecting on what they have learnt. Get them to write it down; to say what new skill they have acquired and in what context can they use them.. 

Ask them what they have understood and what they still don’t understand yet. Make it clear to them it is ok if they don’t have answers or comments, because you can help, but that you are interested and excited to know what their thinking is too. 

Structured Reflection

In the following lesson discuss the previous lesson and how it went. You may recognise these suggested questions are inspired by Bloom’s taxonomy. and identifying the different levels of understanding that are exhibited by each level. 

Remembering

List 3 things you remember from today; one new skill you learnt; which skills have you used in this lesson?

Understanding

What are the most common mistakes people probably make when learning this topic? What is the most important thing we need to know when learning about this topic?

Applying

How could you use what you learnt here in other areas of maths? When might you use this knowledge in real life?

Analysing

What made the learning easier? Explain how the strategies you used were successful.

Evaluating

How efficient were the strategies used to find the answer? Which part of this lesson do you feel you did really well on? Which part of this lesson did you find the hardest?

Creating

Can you thik of other strategies you might have used when calculating …..? How would you check if someone had understood this lesson?

I hope you find reading this information a good use of your time. Please keep coming back for more. If you happen to be someone who wants to study math(s) intelligently so that you can become an independent learner, please contact me. Fill in the application form to book an Empower Hour FREE of charge and let’s get started.